https://github.com/Engelberg/ubergraph.git
git clone 'https://github.com/Engelberg/ubergraph.git'
(ql:quickload :Engelberg.ubergraph)
Ubergraph is a versatile, general-purpose graph data structure for Clojure. It is designed to be compatible with Loom, another popular Clojure collection of graph protocols and algorithms, but it does not require knowledge of Loom to use.
Ubergraph is a great choice for people who:
Add the following line to your leiningen dependencies:
[ubergraph "0.8.1"]
Require ubergraph in your namespace header:
(ns example.core
(:require [ubergraph.core :as uber]))
Ubergraph lists loom as a dependency, so when you add ubergraph to your project, leiningen will also download loom. This means all of loom's namespaces are also available to you in your program. Loom is currently organized in a way that its protocols are split across several different namespaces. As a convenience, ubergraph.core provides access to all of loom's protocol functions through its own namespace.
For example, rather than calling loom.graph/out-edges and loom.attr/add-attr, you can just call uber/out-edges and uber/add-attr.
Ubergraph is tested on Clojure 1.10. Some of the graph algorithms require Java 8 or greater.
When you are done reading this README, check out the Codox-generated docs for the Ubergraph API.
There are four flavors of Ubergraphs: graph, digraph, multigraph, and multidigraph. All share the same underlying representation, but have different default behaviors with respect to adding new edges and attributes. Specifically:
Graphs and Digraphs do not allow duplicate or “parallel” edges, whereas Multigraphs and Multidigraphs do.
Digraphs and Multidigraphs, by default, treat new edge definitions as directed/one-way edges, whereas Graphs and Multigraphs, by default, treat new edge definitions as bidirectional. It is possible, however, to override this default behavior and add directed edges to an undirected graph, and undirected edges to a directed graph.
| Allows parallel edges |
No parallel edges |
|
|---|---|---|
| Directed Edges (by default) |
Multidigraph | Digraph |
| Undirected Edges (by default) |
Multigraph | Graph |
All ubergraph constructors are multiple arity functions that can take an arbitrary number of “inits” where an init is defined as one of:
Edge description inits automatically add the src and dest nodes, so you don't need to specify nodes explicitly unless you want to create an isolated, unconnected node, or you want to use the [node attribute-map] form to initialize a node with a given attribute map.
It is often convenient that the ubergraph constructors can take so many different kinds of “inits”, but as you can see, there is some inherent ambiguity. Should we interpret [{:a 1} {:b 2}] as a node labeled [{:a 1} {:b 2}], or as a node {:a 1} with attribute map {:b 2}, or as an edge between two nodes {:a 1} and {:b 2}? In this particular case, Ubergraph would interpret the ambiguous init as a [node attribute-map] form (resolution of conflicts is in the order listed above), but you can force the other interpretations by adding ^:node or ^:edge metadata, i.e., ^:node [{:a 1} {:b 2}] would be interpreted as a node labeled [{:a 1} {:b 2}] and ^:edge [{:a 1} {:b 2}] would be interpreted as an edge between two nodes. Alternatively, you can construct an empty ubergraph and build it up with the unambiguous functions add-nodes, add-nodes-with-attrs, or add-edges.
Ubergraphs built with the graph constructor treat every edge as a bidirectional, undirected edge.
(def graph1
(uber/graph [:a :b] [:a :c] [:b :d]))
=> (uber/pprint graph1)
Graph
4 Nodes:
:d
:c
:b
:a
3 Edges:
:b <-> :d
:a <-> :c
:a <-> :bEdge definitions can include weights.
(def graph2
(uber/graph [:a :b 2] [:a :c 3] [:b :d 4]))
=> (uber/pprint graph2)
Graph
4 Nodes:
:d
:c
:b
:a
3 Edges:
:b <-> :d {:weight 4}
:a <-> :c {:weight 3}
:a <-> :b {:weight 2}Note that ubergraph differs from Loom in the way that it handles weights. Ubergraph simply stores weights in the edge's attribute map, under the keyword :weight. In my opinion, this is a superior way to handle weights because it allows you to manipulate weights using the same interface that you use to alter other attributes. Also, once weight is no longer a privileged field, it makes it easier to develop algorithms that take as an additional input the attribute to use as the edge weight. Right now, Loom algorithms have a baked-in notion that we only want to do traversals based on weight, and this is a problem. Ideally, we want it to be just as easy to search a graph for shortest traversals using other attributes such as :price or :distance. However, to be compatible with Loom's protocols, Ubergraphs support the protocol function weight which simply extracts the :weight attribute from the attribute map.
(def graph3
(uber/graph [:a :b {:weight 2 :price 200 :distance 10}]
[:a :c {:weight 3 :price 300 :distance 20}]))
=> (uber/pprint graph3)
Graph
3 Nodes:
:c
:b
:a
2 Edges:
:a <-> :c {:weight 3, :price 300, :distance 20}
:a <-> :b {:weight 2, :price 200, :distance 10}You can extend graphs with more “inits” by using build-graph, or you can use add-nodes, add-nodes-with-attrs (which takes only [node attr-map] inits), or add-edges (which takes [src dest], [src dest weight], or [src dest attr-map] inits). add-nodes*, add-nodes-with-attrs* and add-edges* are variants which take sequences rather than multiple args.
(build-graph graph1 [:d :a] [:d :e])
(add-edges graph1 [:d :a] [:d :e])
(add-edges* graph1 [[:d :a] [:d :e]])
(add-nodes graph1 :e)
(add-nodes* graph1 [:e])
(add-nodes-with-attrs graph1 [:a {:happy true}] [:b {:sad true}])
(add-nodes-with-attrs* graph1 [[:a {:happy true}] [:b {:sad true}]])Adding nodes that already exist will do nothing. Basic graphs that are not multigraphs do not permit “parallel edges”, so adding edges that already exist will cause the new attribute map to be merged with the existing one. However, if you really want to, you can add a directed edge to an undirected graph with add-directed-edges or add-directed-edges*:
=> (uber/pprint (uber/add-directed-edges graph1 [:a :d]))
Graph
4 Nodes:
:d
:c
:b
:a
4 Edges:
:b <-> :d
:a -> :d
:a <-> :c
:a <-> :bUbergraph supports all of Loom's protocols, so you can do all the things you'd expect to be able to do to graphs: nodes, edges, has-node?, has-edge?, successors, out-degree, out-edges, predecessors, in-degree, in-edges, transpose, weight, add-nodes, add-nodes*, add-edges, add-edges*, remove-nodes, remove-nodes*, remove-edges, remove-edges*, and remove-all.
Ubergraph also supports the ability to lookup attributes on any node or edge in the graph with attr and attrs, add attributes with add-attr and add-attrs, remove attributes with remove-attr and remove-attrs, and set the attribute map (overwriting the existing attribute map) with set-attrs. It is not a good idea to add/set/remove attributes for a node or edge that doesn't exist in the graph. Create the node or edge first and then manipulate its attributes, or build your graph with functions that allow you to set up the attributes at the same time you add nodes and edges.
One way that Ubergraph improves upon Loom is that graph edges have a richer implementation and support additional abstractions. This richer implementation is what allows directed and undirected edges to coexist, and allows for parallel edges in multigraphs. So where Loom functions return [src dest] tuples or [src dest weight] tuples to represent edges, Ubergraph returns actual Edge or UndirectedEdge objects. For example,
=> (-> (uber/graph [:a :b])
(uber/add-directed-edges [:a :c])
uber/edges)
(#ubergraph.core.UndirectedEdge{:id #uuid "8a8a69a4-f7b9-4992-b752-c3d976a32f21",
:src :b, :dest :a, :mirror? true}
#ubergraph.core.Edge{:id #uuid "5341be54-e501-4bcb-b22d-5fbcb5c828df",
:src :a, :dest :c}
#ubergraph.core.UndirectedEdge{:id #uuid "8a8a69a4-f7b9-4992-b752-c3d976a32f21",
:src :a, :dest :b, :mirror? false})The main thing to note here is that internally, all edges have a :src field, a :dest field, and a uuid, which you can think of as a pointer to the map of attributes for that edge. The other thing to note is that undirected edges are stored internally as a pair of edge objects, one for each direction. Both edges of the pair share the same id (and therefore, the same attribute map) and one of the edges is marked as a “mirror” edge. This is critical because in some algorithms, we want to traverse over all edges in both directions, but in other algorithms we only want to traverse over unique edges. Loom provides no mechanism for this, but Ubergraph makes this easy with the protocol function mirror-edge?, which returns true for the mirrored edge in an undirected pair of edges, and false for directed edges and the non-mirrored undirected edges. So (edges g) gives you all the edges in a graph, and (remove mirror-edge? (edges g)) would give you a sequence of unique edges, without listing both directions of the same undirected edge.
When writing algorithms over edges, it is strongly recommended that you access the edge endpoints through the edge abstraction, using the protocol functions src and dest (although edges returned by Loom protocols support [src dest] and [src dest weight] destructuring for backwards compatibility with Loom). Edges also support the protocol functions edge?, directed-edge?, undirected-edge?, and other-direction (which returns the other edge in the pair for undirected edges, or nil if it is a directed edge).
Digraphs (short for “directed graphs”) are built with the digraph constructor. Digraphs behave similarly to Graphs, but by default, they add edges as one-way directed edges. All the same functions apply to directed graphs. You can add undirected edges to a directed graph with add-undirected-edges or add-undirected-edges*.
Multigraphs (built with the multigraph constructor) allow “parallel edges” between pairs of nodes. This is where Ubergraph really shines over Loom. The crux of the problem with Loom is that throughout Loom's implementation, the protocols and algorithms are hardcoded with the notion that an edge is uniquely described by its source and destination. This completely breaks down when you're dealing with multigraphs.
We've already seen one way that Ubergraph solves this problem: Ubergraph identifies edges not only by a src and a dest, but also by a unique id. This allows it to store multiple edges between a given src and dest, each with its own id which can be used to look up its set of attributes.
But there are also many functions which require some description of an edge as an input. Describing an edge as a [src dest] pair is not enough. When multiple edges can have the same src and dest, we need a richer way to identify a given edge.
In addition to edge objects (Edge or UndirectedEdge), Ubergraph introduces the notion of an “edge description”. An edge description is one of the following:
Every Loom protocol that takes a simple [src dest] input to describe an edge, in Ubergraph can either take an edge object or one of these edge descriptions.
If you use an edge description, it's up to you to pick an edge description that uniquely identifies your edge. If your graph contains multiple edges that match a given edge description, ubergraph will arbitrarily pick one such edge for you. For example, if your multigraph uses different colors to represent several edges between a given pair of nodes, then the edge description [1 4 {:color :red}] might be unambiguous for your application. Using the actual edge object is, of course, the easiest way to ensure you are unqiuely identifying the edge.
For example,
(weight g [1 4 {:color :red}]) ; what is the weight of the red edge between 1 and 4?
(attr g [:a :b 5] :color) ; what is the color of the edge from :a to :b with weight 5?In a multigraph, finding all the edges with a given property is of paramount importance. So Ubergraph, supports the notion of “edge queries”. The most common such query is:
(find-edges g :a :b)which means, “find all the edges from :a to :b”.
But find-edges also supports an arbitrary query-map, which is an attribute map plus, optionally, :src and/or :dest keys to narrow down the search, for example:
(find-edges g {:src :a, :dest :b, :weight 5})
(find-edges g {:dest :b, :size :large})
(find-edges g {:color :red})When you don't supply :src and :dest, the query won't be particularly efficient, but at least the capability is there. find-edges returns a sequence of edge objects, which can be used as unambiguous edge descriptions to look up other attributes, remove the edges, etc.
find-edge takes the same inputs as find-edges but just returns the first match.
Multidigraphs, as you'd expect, are built with the multidigraph constructor and are the directed-as-default version of multigraphs.
The general-purpose ubergraph constructor takes two booleans (allow-parallel-edges? and undirected-graph?) and dispatches to the appropriate constructor. So:
(ubergraph true true ...) calls multigraph(ubergraph true false ...) calls multidigraph(ubergraph false true ...) calls graph(ubergraph false false ...) calls digraphYou can test to find out what kind of ubergraph you have with the predicates allow-parallel-edges? and undirected-graph?. (Keep in mind that undirected-graph? just tests whether new edges are added as undirected by default. You can override this behavior for specific edges.)
Nodes are used internally as keys in Clojure maps within Ubergraph's implementation, so you should pick values to represent nodes that work as keys in hash maps. Any Clojure immutable values where Clojure's hash function is consistent with = will work, which includes most immutable values, i.e. numbers, strings, keywords, and Clojure vectors, maps, sets, and sequences that contain only immutable values. See Clojure's Equality guide for a handful of exceptions. Both Loom and Ubergraph will give incorrect return results for some functions if you use nil or false as a node value, so it is strongly recommended that you avoid using them as nodes.
The attributes of a node are stored inside the graph value. They are not somehow “attached” to nodes independently of a graph. Thus node attributes are independent in different graphs, even if those graphs use the same values to represent nodes. The same goes for the attributes of edges; they are stored inside the graph value.
Although node and edge attributes are stored inside of the graph value, sometimes it is useful to have a “view” of the node or edge that includes the attribute map. Ubergraph provides convenience functions to do just that: node-with-attrs (which takes a graph and node and returns [node attribute-map]) and edge-with-attrs (which takes a graph and edge object or edge description, and returns [src dest attribute-map]).
Examples:
(node-with-attrs g :a) => [:a {:color :red}]
(edge-with-attrs g #ubergraph.core.Edge{:id #uuid "5341be54-e501-4bcb-b22d-5fbcb5c828df",
:src :a, :dest :c}) => [:a :c {:weight 10}]There are two common uses for these convenience functions:
(for [[src dest attrs] (map (partial edge-with-attrs g) (edges g))]
...)(add-edges* g1 (map (partial edge-with-attrs g2) (edges g2)))Note that the output of node-with-attrs and edge-with-attrs is annotated with metadata so it can be safely and unambiguously recognized as a node or edge description if passed to the build-graph function.
Edges are represented as a pair of nodes plus an internally generated UUID that serves as the unique identifier of the edge's attribute map. The use of UUIDs ensures that every newly created edge is unique. There are several functions that allow you to create new edges using an edge description, specifying a pair of nodes plus optional attributes. These functions create fresh edge objects with fresh UUIDs assigned to avoid any possible conflict between edges.
While edge objects returned via find-edge (and other functions) are immutable values, don't add ubergraph's edge objects as nodes to the same or other graphs; this is not supported. In particular, this can cause problems with attributes.
As you build up graphs, random uuids are generated to link edges to attributes. This randomness means that two graphs which are semantically equal might not necessarily be structurally equal in the Clojure sense. The hashing and equality for Ubergraphs has been overridden to reflect an intuitive notion of equality, so you can trust, for example that (= (graph [1 2]) (graph [1 2])) even though the two graphs contain different uuids.
Two Ubergraph graphs g1 and g2 are equal if all of the following are true:
g1 and g2 have the same set of node values.n, the entire attribute map of n in g1 is equal to the entire attribute map of n in g2n1, n2, the edge(s) between them, ignoring edge uuids, but including the directionality and the entire attribute map for every edge, is equal. For graphs allowing parallel edges, these are compared as multisets, i.e. if g1 has 3 edges with attribute map {:label 17} and 2 edges with an empty attribute map, then g2 must also have 3 edges with attribute map {:label 17} and 2 edges with an empty attribute map, to be equal to g1.Graph ismorphism is a more general idea of equality between graphs, in which nodes can be “relabeled” before comparing to see if they have the same edges. That is a much more computationally expensive idea of graph equality to determine, and is not what Ubergraph = between graphs determines. Thus (= (graph [1 2]) (graph [2 3])) is false, even though they both have two nodes with a single edge between them, so they would be considered isomorphic.
The ubergraph.alg namespace contains a variety of useful graph algorithms. Some of these algorithms are lifted directly from Loom – because Ubergraph implements Loom's protocols, many of Loom's algorithms work seamlessly on Ubergraphs. Some of the algorithms that come directly from Loom include: connected-components, connected?, pre-traverse, pre-span, post-traverse, topsort, bf-span, dag?, scc, strongly-connected?, connect, bipartite-color, bipartite?, bipartite-sets. Some algorithms were adapted from Loom for Ubergraphs with only very minor tweaks, such as loners, distinct-edges, and longest-shortest-path.
However, Ubergraph's Multigraphs and Multidigraphs go far beyond Loom's capabilities, allowing for algorithms with parallel edges. Most of Loom's path-finding algorithms fail to take into account the possibility of parallel edges. For example, Loom returns its paths as a list of nodes you visit. This is sufficient when there is at most one edge between a given pair of nodes, but in a multigraph, it is absolutely necessary to identify precisely which edge you are traveling along.
For this reason, the ubergraph.alg namespace implements a brand-new shortest-path algorithm that is rich with functionality. Ubergraph's shortest-path algorithm returns paths, which implement a protocol (also found in ubergraph.alg) that allows you get to the following information about a path: edges-in-path, nodes-in-path, cost-of-path (with respect to the kind of search that generated the path), start-of-path, and end-of-path.
To appreciate the power of Ubergraph's shortest-path function, let's take a look at several examples. But first, for reference, here is the docstring of shortest-path:
Finds the shortest path in graph g. You must specify a start node or a collection
of start nodes from which to begin the search, however specifying an end node
is optional. If an end node condition is specified, this function will return an
implementation of the IPath protocol, representing the shortest path. Otherwise,
it will search out as far as it can go, and return an implementation of the
IAllPathsFromSource protocol, which contains all the data needed to quickly find
the shortest path to a given destination (using IAllPathsFromSource's `path-to`
protocol function).
If :traverse is set to true, then the function will instead return a lazy sequence
of the shortest paths from the start node(s) to each node in the graph in the order
the nodes are encountered by the search process.
Takes a search-specification map which must contain:
Either :start-node (single node) or :start-nodes (collection)
Map may contain the following entries:
Either :end-node (single node) or :end-nodes (collection) or :end-node? (predicate function)
:cost-fn - A function that takes an edge as an input and returns a cost
(defaults to every edge having a cost of 1, i.e., breadth-first search if no cost-fn given)
:cost-attr - Alternatively, can specify an edge attribute to use as the cost
:heuristic-fn - A function that takes a node as an input and returns a
lower-bound on the distance to a goal node, used to guide the search
and make it more efficient.
:node-filter - A predicate function that takes a node and returns true or false.
If specified, only nodes that pass this node-filter test will be considered in the search.
:edge-filter - A predicate function that takes an edge and returns true or false.
If specified, only edges that pass this edge-filter test will be considered in the search.
Map may contain the following additional entries if a traversal sequence is desired:
:traverse true - Changes output to be a sequence of paths in order encountered.
:min-cost - Filters traversal sequence, only applies if :traverse is set to true
:max-cost - Filters traversal sequence, only applies if :traverse is set to true
shortest-path has specific arities for the two most common combinations:
(shortest-path g start-node end-node)
(shortest-path g start-node end-node cost-attr)OK, that's a bit of a doozy, but it helps give an idea of how much this one function can do. You may have noticed that several of the parameters refer to cost, such as :cost-fn, :cost-attr, :min-cost, and :max-cost. Ubergraph uses the term cost as a generalization of what Loom calls weight. In Loom, all the search algorithms only work on weight; in Ubergraph, I picked a new term, cost, to emphasize that you are not restricted to searching on weight, and can use any other attribute or function of edges. And in a breadth-first search, your “cost” is the number of edges. This will hopefully become more clear with examples.
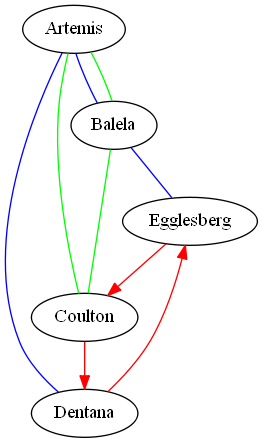
For our first running example, let's consider this map of the fictitious country of Altopia, serviced by three airlines.

This map was generated from the following graph:
(def airports
(-> (uber/multigraph
; city attributes
[:Artemis {:population 3000}]
[:Balela {:population 2000}]
[:Coulton {:population 4000}]
[:Dentana {:population 1000}]
[:Egglesberg {:population 5000}]
; airline routes
[:Artemis :Balela {:color :blue, :airline :CheapAir, :price 200, :distance 40}]
[:Artemis :Balela {:color :green, :airline :ThriftyLines, :price 167, :distance 40}]
[:Artemis :Coulton {:color :green, :airline :ThriftyLines, :price 235, :distance 120}]
[:Artemis :Dentana {:color :blue, :airline :CheapAir, :price 130, :distance 160}]
[:Balela :Coulton {:color :green, :airline :ThriftyLines, :price 142, :distance 70}]
[:Balela :Egglesberg {:color :blue, :airline :CheapAir, :price 350, :distance 50}])
(uber/add-directed-edges
[:Dentana :Egglesberg {:color :red, :airline :AirLux, :price 80, :distance 50}]
[:Egglesberg :Coulton {:color :red, :airline :AirLux, :price 80, :distance 30}]
[:Coulton :Dentana {:color :red, :airline :AirLux, :price 80, :distance 65}])))
=> (uber/pprint airports)
Multigraph
5 Nodes:
:Egglesberg {:population 5000}
:Dentana {:population 1000}
:Coulton {:population 4000}
:Balela {:population 2000}
:Artemis {:population 3000}
9 Edges:
:Egglesberg -> :Coulton {:airline :AirLux, :color :red, :price 80, :distance 30}
:Dentana -> :Egglesberg {:airline :AirLux, :color :red, :price 80, :distance 50}
:Coulton -> :Dentana {:airline :AirLux, :color :red, :price 80, :distance 65}
:Balela <-> :Egglesberg {:airline :CheapAir, :color :blue, :price 350, :distance 50}
:Balela <-> :Coulton {:airline :ThriftyLines, :color :green, :price 142, :distance 70}
:Artemis <-> :Dentana {:airline :CheapAir, :color :blue, :price 130, :distance 160}
:Artemis <-> :Coulton {:airline :ThriftyLines, :color :green, :price 235, :distance 120}
:Artemis <-> :Balela {:airline :CheapAir, :color :blue, :price 200, :distance 40}
:Artemis <-> :Balela {:airline :ThriftyLines, :color :green, :price 167, :distance 40}To create a visualization of the graph, I used the viz-graph function in the ubergraph.core namespace (must have GraphViz installed for this to work):
=> (uber/viz-graph airports)To save it to a file, I did the following:
clojure
=> (uber/viz-graph airports {:save {:filename "C:/temp/airports.png" :format :png}})
The options map for viz-graph can also take a Graphviz layout algorithm (e.g., :neato) with, for example, :layout :neato. Another option is to specify :auto-label true which will annotate all the nodes and edges with their attribute maps. If the attribute maps for the nodes and edges contain attributes relevant to Graphviz (e.g., color, style, etc.) then graphviz will take that into account when drawing the graph.
So let's start off with a simple question: What is the trip with the fewest hops from Artemis to Egglesberg? This calls for a breadth-first search, and this is what shortest-path does by default. We require the ubergraph.alg namespace and alias it as alg. ubergraph.alg contains both the shortest-path algorithm, as well as all the functions that operate on paths.
=> (alg/shortest-path airports {:start-node :Artemis, :end-node :Egglesberg})
#ubergraph.alg.Path{:list-of-edges #<Delay@328ab9ec: :pending>, :cost 2, :end :Egglesberg,
:last-edge #ubergraph.core.UndirectedEdge{:id #uuid "827f7769-db20-45c4-b3d9-272f47e87bcc",
:src :Balela,
:dest :Egglesberg,
:mirror? false}}Hmm, that doesn't seem overly useful. But remember, paths implement a protocol that lets us get at the details of the path:
=> (alg/nodes-in-path (alg/shortest-path airports {:start-node :Artemis, :end-node :Egglesberg}))
(:Artemis :Dentana :Egglesberg)
=> (alg/edges-in-path (alg/shortest-path airports {:start-node :Artemis, :end-node :Egglesberg}))
(#ubergraph.core.UndirectedEdge{:id #uuid "4e79cfc4-e15d-42ed-8cf6-44476f2ed972",
:src :Artemis, :dest :Dentana, :mirror? false}
#ubergraph.core.Edge{:id #uuid "4f1b2958-c355-4512-a5ca-9e89f5f49207",
:src :Dentana, :dest :Egglesberg})
=> (alg/start-of-path (alg/shortest-path airports {:start-node :Artemis, :end-node :Egglesberg}))
:Artemis
=> (alg/end-of-path (alg/shortest-path airports {:start-node :Artemis, :end-node :Egglesberg}))
:Egglesberg
=> (alg/cost-of-path (alg/shortest-path airports {:start-node :Artemis, :end-node :Egglesberg}))
2
=> (alg/last-edge-of-path (alg/shortest-path airports {:start-node :Artemis, :end-node :Egglesberg}))
#ubergraph.core.UndirectedEdge{:id #uuid "827f7769-db20-45c4-b3d9-272f47e87bcc",
:src :Balela,
:dest :Egglesberg,
:mirror? false}The edges don't directly store the attributes (they are stored in the graph, keyed by edge id). A convenience function is provided to make it easy to see from a glance at the REPL which edges we're talking about:
=> (alg/pprint-path (alg/shortest-path airports {:start-node :Artemis, :end-node :Egglesberg}))
Total Cost: 2
:Artemis -> :Dentana {:airline :CheapAir, :color :blue, :price 130, :distance 160}
:Dentana -> :Egglesberg {:airline :AirLux, :color :red, :price 80, :distance 50}Note that in this case, the cost is referring to the number of edges we traversed (since we did a breadth-first search), which means that there are two edges in the path.
Another possibility is to roll your own function to supply the important details of your edges:
(def airport-edge-details (juxt uber/src uber/dest #(uber/attr airports % :airline)))
=> (->> (alg/shortest-path airports {:start-node :Artemis, :end-node :Egglesberg})
alg/edges-in-path
(map airport-edge-details))
([:Artemis :Dentana :CheapAir] [:Dentana :Egglesberg :AirLux])A breadth-first search between two specific nodes is one of the most common ways to call this function, so the 3-arity version of shortest-path supports this use case directly. The above question could also have been written as:
=> (alg/shortest-path airports :Artemis :Egglesberg)What is the trip that is the shortest distance from Coulton to Egglesberg? We can answer this by setting the :cost-attr to be :distance.
=> (alg/pprint-path (alg/shortest-path airports {:start-node :Coulton, :end-node :Egglesberg, :cost-attr :distance}))
Total Cost: 115
:Coulton -> :Dentana {:airline :AirLux, :color :red, :price 80, :distance 65}
:Dentana -> :Egglesberg {:airline :AirLux, :color :red, :price 80, :distance 50}Note that because we searched by distance the total “Cost” that is printed is the total distance.
A cost-attribute search between two nodes is the second-most common query, so you can express it more compactly as:
clojure
(alg/shortest-path airports :Coulton :Egglesberg :distance)
One really nice aspect of Ubergraph is that, unlike Loom, which has a single privileged “weight” field that you can search on, Ubergraph makes it just as easy to search on any attribute. What is the cheapest trip from Artemis to Egglesberg?
=> (alg/pprint-path (alg/shortest-path airports :Artemis :Egglesberg :price))
Total Cost: 210
:Artemis -> :Dentana {:airline :CheapAir, :color :blue, :price 130, :distance 160}
:Dentana -> :Egglesberg {:airline :AirLux, :color :red, :price 80, :distance 50}In this case, because we searched on :price, the “Cost” that is printed is actually the price.
Actually, we are not just limited to minimizing based on edge attributes, we can also search by any arbitrary cost function that takes an edge as its input. Let's use this power to find out the best way to get from Artemis to Egglesberg if we want to prioritize the shortest number of edges and use distance as a tiebreaker. We can do this by creating a function that imposes a large cost on each edge, and a small additional cost based on distance.
=> (alg/pprint-path
(alg/shortest-path airports
{:start-node :Artemis, :end-node :Egglesberg,
:cost-fn (fn [e] (+ 100000 (uber/attr airports e :distance)))}))
Total Cost: 200090
:Artemis -> :Balela {:airline :ThriftyLines, :color :green, :price 167, :distance 40}
:Balela -> :Egglesberg {:airline :CheapAir, :color :blue, :price 350, :distance 50}Let's say I plan to do a lot of travel out of Coulton, and I plan to search for the shortest distance path from Coulton to several other cities. If I just pass shortest-path a start node with no end node, it will return an instance of the AllPathsFromSource protocol, which can essentially be thought of as a lookup table that can be used to efficiently answer shortest paths questions emanating from the same source.
(def out-of-coulton (alg/shortest-path airports {:start-node :Coulton, :cost-attr :distance}))We extract the specific paths with the path-to protocol function.
=> (alg/pprint-path (alg/path-to out-of-coulton :Artemis))
Total Cost: 110
:Coulton -> :Balela {:airline :ThriftyLines, :color :green, :price 142, :distance 70}
:Balela -> :Artemis {:airline :ThriftyLines, :color :green, :price 167, :distance 40}What are all the places we can get to from Couton?
=> (alg/all-destinations out-of-coulton)
(:Balela :Artemis :Coulton :Egglesberg :Dentana)Sometimes, you don't just want the final lookup table of paths, you want to see the order in which the paths are discovered by the search process. You can get this sequence of paths by setting :traverse true. Let's look at the order in which the cities are visited in a breadth-first search out of Artemis. Remember, this is a sequence of path objects that is returned, so we can use any of the path protocol functions to get at the contents of the path.
=> (alg/shortest-path airports {:start-node :Artemis, :traverse true})
(#ubergraph.alg.Path{:list-of-edges #<Delay@7d3b1918: :pending>, :cost 0, :end :Artemis, :last-edge ...}
#ubergraph.alg.Path{:list-of-edges #<Delay@5462d913: :pending>, :cost 1, :end :Dentana, :last-edge ...}
#ubergraph.alg.Path{:list-of-edges #<Delay@410fe1e3: :pending>, :cost 1, :end :Coulton, :last-edge ...}
#ubergraph.alg.Path{:list-of-edges #<Delay@507f93c7: :pending>, :cost 1, :end :Balela, :last-edge ...}
#ubergraph.alg.Path{:list-of-edges #<Delay@75a9a309: :pending>, :cost 2, :end :Egglesberg, :last-edge ...})We can place minimum and maximum cost constraints on the sequence of paths returned by the traversal. So, for example, if we want to know all the cities who are (at best) two hops from Egglesberg:
=> (map alg/end-of-path
(alg/shortest-path airports
{:start-node :Egglesberg, :traverse true, :min-cost 2, :max-cost 2}))
(:Dentana :Artemis)shortest-path allows you filter the edges and nodes. What is the fewest hops from Dentana to Egglesberg avoiding the airline AirLux?
(alg/shortest-path airports
{:start-node :Dentana, :end-node :Egglesberg,
:edge-filter (fn [e] (not= :AirLux (uber/attr airports e :airline)))})What is the shortest distance from Egglesberg to Artemis, going only through large cities (population at least 3000)?
(alg/shortest-path airports
{:start-node :Egglesberg, :end-node :Artemis,
:node-filter (fn [n] (<= 3000 (uber/attr airports n :population))),
:cost-attr :distance})You can specify more than one start node. Let's say I live halfway between Artemis and Balela and can use either airport. What is the cheapest way to get from either of those airports to Dentana?
clojure
(alg/shortest-path airports {:start-nodes [:Artemis :Balela], :end-node :Dentana, :cost-attr :price})
You can specify more than one end node. Let's say my sister is coming to visit me from Dentana, which airport should she fly into to save money?
clojure
(alg/shortest-path airports {:start-node :Dentana, :end-nodes [:Artemis :Balela], :cost-attr :price})
Instead of listing specific end nodes, you can provide a predicate function to test whether a node qualifies as an end node. What is the cheapest way to get from Coulton to any small city for a weekend getaway?
clojure
(alg/shortest-path airports {:start-node :Coulton,
:end-node? (fn [n] (> 3000 (uber/attr airports n :population))),
:cost-attr :price})
shortest-path also has built into it the ability to do an A-star search, which uses a heuristic function to make the search more efficient. For this to work, the heuristic function must take a node and return a lower bound on the cost of the path between the node and the end node(s). So, for example, a function that always returns 0 would be a valid heuristic function, but wouldn't help make the search more efficient.
To demonstrate this feature, I created a graph that links all five-letter words that have only a one-letter change between them. This graph can be used to construct “word ladders”.
=> (time (alg/nodes-in-path (alg/shortest-path wg "amigo" "enter")))
"Elapsed time: 25.430857 msecs"
("amigo" "amino" "amine" "amide" "abide" "abode" "anode" "anole" "anile" "anise" "arise" "prise" "prime" "prims" "pries" "prier" "pryer" "payer" "pater" "eater" "enter")Clearly, a lower-bound on how far a word is from another word is the number of letters that are different between the words (since you can only change one letter at a time).
(defn word-edit-distance [w1 w2]
(apply + (for [[l1 l2] (map vector w1 w2),
:when (not= l1 l2)]
1)))
=> (time (alg/nodes-in-path (alg/shortest-path wg
{:start-node "amigo" :end-node "enter"
:heuristic-fn #(word-edit-distance % "enter")})))
"Elapsed time: 5.223978 msecs"
("amigo" "amino" "amine" "amide" "abide" "abode" "anode" "anole" "anile" "anise" "arise" "prise" "prime" "prims" "pries" "prier" "pryer" "payer" "pater" "eater" "enter")By supplying the heuristic function, we were able to cut down the search time.
Last but not least, shortest-path can handle edges with negative costs. If it detects a negative cost, it will run the bellman-ford algorithm, which is somewhat slower, but produces the correct results with negative edges.
(def negative-weight-example
(uber/digraph
[:s :a 5]
[:s :c -2]
[:c :a 2]
[:c :d 3]
[:a :b 1]
[:b :c 2]
[:b :d 7]
[:b :t 3]
[:d :t 10]))
=> (alg/shortest-path negative-weight-example :s :b :weight)
#ubergraph.alg.Path{:list-of-edges #<Delay@7a3ed5ab: :pending>, :cost 1, :end :b, :last-edge ...}Note: If you call shortest-path on a graph with a negative-weight cycle, the function will return false.
All of Ubergraph's algorithms, including the new shortest-path, should be backwards-comaptible with Loom's graphs.
The above section discussed how to search for shortest paths within a graph. But sometimes you want to go the other way, and let a search process drive the construction of a graph. This comes up a lot in my own work: I'm solving a puzzle and I know the start state and an end state, and I know the rules for state transitions, but I have no idea how I'm going to get from the start state to end state. I want to search for a path from the start state to the end state, even though I don't yet know all the nodes of the graph.
The docstring given in the previous section for shortest-path was slightly simplified. It actually begins as follows:
Finds the shortest path in g, where g is either an ubergraph or a
transition function that implies a graph. A transition function
takes the form: (fn [node] [{:dest successor1, ...} {:dest successor2, ...} ...])So, you can do a search simply by passing in a function that tells you all the nodes you can reach from a given node. The way you do this is with a function that takes a node as an input and returns a sequence of maps as the output. You can think of this function as a way of specifying all the edges coming out of the input node. Each map must have a :dest key, which tells you the destination node of the edge. Any other key-value pairs in the map will be attached to the edge as attributes (this allows you to specify weights or other useful information to guide the search or label the results).
As an example, let's consider a graph where the nodes are all the natural numbers, and there are two types of edges: incrementing a number by one or doubling it. As you can see, this is an infinite graph, and therefore, can't be expressed as an ubergraph. But we can still do a meaningful search on the transition function:
=> (-> (alg/shortest-path (fn [n] [{:dest (* n 2) :label :double}
{:dest (inc n) :label :increment}])
1 19)
alg/pprint-path)
Total Cost: 6
1 -> 2 {:label :double}
2 -> 4 {:label :double}
4 -> 8 {:label :double}
8 -> 9 {:label :increment}
9 -> 18 {:label :double}
18 -> 19 {:label :increment}Note that since we're searching using a function rather than searching within Ubergraph, when we call edges-in-path, there are no actual Edge objects to return, so instead you get back edge descriptions, i.e., vectors of the form [src dest attribute-map].
=> (-> (alg/shortest-path (fn [n] [{:dest (* n 2) :label :double, :weight 3}
{:dest (inc n) :label :increment, :weight 1}])
{:start-node 1, :end-node 19, :cost-attr :weight})
alg/edges-in-path)
([1 2 {:label :increment, :weight 1}]
[2 3 {:label :increment, :weight 1}]
[3 4 {:label :increment, :weight 1}]
[4 8 {:label :double, :weight 3}]
[8 9 {:label :increment, :weight 1}]
[9 18 {:label :double, :weight 3}]
[18 19 {:label :increment, :weight 1}])But it's clear that it would be possible to derive an ubergraph from the edge descriptions produced by the search process. And the function paths->graph does exactly that. It works on the output produced shortest-path. Recall that shortest-path can produce either a single path, or a sequence of paths when called with :traverse true, or an IAllPathsFromSource object when no end criterion is given. paths->graph will work on any of those output types. On a single path, you'll get back the graph with exactly those edges. But where it gets really interesting is when shortest-path returns one of the other two output types.
When shortest-path is called with :traverse true, then paths->graph gives you insight into exactly which edges were explored during the search process, and captures all those transition edges as a new graph.
=> (-> (alg/shortest-path (fn [n] [{:dest (* n 2) :label :double}
{:dest (inc n) :label :increment}])
{:start-node 1, :end-node 9, :traverse true})
alg/paths->graph uber/pprint)
Digraph
9 Nodes:
1 {:cost-of-path 0}
4 {:cost-of-path 2}
6 {:cost-of-path 3}
3 {:cost-of-path 2}
2 {:cost-of-path 1}
9 {:cost-of-path 4}
5 {:cost-of-path 3}
16 {:cost-of-path 4}
8 {:cost-of-path 3}
8 Edges:
1 -> 2 {:label :double}
4 -> 8 {:label :double}
4 -> 5 {:label :increment}
3 -> 6 {:label :double}
2 -> 4 {:label :double}
2 -> 3 {:label :increment}
8 -> 16 {:label :double}
8 -> 9 {:label :increment}Best of all, when shortest-path is called with no end condition specified, then paths->graph will capture the entire state space reachable from the start node(s), and all the transitions explored. In this example, where we're working with an infinite state space and not specifying an end, we'll use a node-filter to constrain the search.
=> (-> (alg/shortest-path (fn [n] [{:dest (* n 2) :label :double}
{:dest (inc n) :label :increment}])
{:start-node 1, :node-filter #(< % 12)})
alg/paths->graph uber/pprint)
Digraph
11 Nodes:
7 {:cost-of-path 4}
1 {:cost-of-path 0}
4 {:cost-of-path 2}
6 {:cost-of-path 3}
3 {:cost-of-path 2}
2 {:cost-of-path 1}
11 {:cost-of-path 5}
9 {:cost-of-path 4}
5 {:cost-of-path 3}
10 {:cost-of-path 4}
8 {:cost-of-path 3}
10 Edges:
1 -> 2 {:label :double}
4 -> 5 {:label :increment}
4 -> 8 {:label :double}
6 -> 7 {:label :increment}
3 -> 6 {:label :double}
2 -> 3 {:label :increment}
2 -> 4 {:label :double}
5 -> 10 {:label :double}
10 -> 11 {:label :increment}
8 -> 9 {:label :increment}There are two options for serializing and deserializing ubergraphs.
The function ubergraph->edn converts an ubergraph to the EDN subset of Clojure, so you can use your favorite EDN serialization mechanism such as nippy or transit, or use something like cheshire to convert it to JSON.
=> (uber/ubergraph->edn graph3)
{:allow-parallel? false,
:undirected? true,
:nodes [[:a {}] [:b {}] [:c {}]],
:directed-edges [],
:undirected-edges [[:a :b {:weight 2, :price 200, :distance 10}] [:a :c {:weight 3, :price 300, :distance 20}]]}You can recover the ubergraph from the EDN with the function edn->ubergraph.
You can create a Clojure-readable string out of an ubergraph as follows:
=> (binding [*print-dup* true] (pr-str graph3))
"#=(ubergraph.core.Ubergraph. #=(clojure.lang.PersistentArrayMap/create {:a #ubergraph.core.NodeInfo[#=(clojure.lang.PersistentArrayMap/create {:b #{#ubergraph.core.UndirectedEdge[#uuid \"9189ba27-1298-411a-910e-3a32245f1489\", :a, :b, false]}, :c #{#ubergraph.core.UndirectedEdge[#uuid \"f18e3829-e53c-4f30-bed8-db5ec9327458\", :a, :c, false]}}), #=(clojure.lang.PersistentArrayMap/create {:b #{#ubergraph.core.UndirectedEdge[#uuid \"9189ba27-1298-411a-910e-3a32245f1489\", :b, :a, true]}, :c #{#ubergraph.core.UndirectedEdge[#uuid \"f18e3829-e53c-4f30-bed8-db5ec9327458\", :c, :a, true]}}), 2, 2], :b #ubergraph.core.NodeInfo[#=(clojure.lang.PersistentArrayMap/create {:a #{#ubergraph.core.UndirectedEdge[#uuid \"9189ba27-1298-411a-910e-3a32245f1489\", :b, :a, true]}}), #=(clojure.lang.PersistentArrayMap/create {:a #{#ubergraph.core.UndirectedEdge[#uuid \"9189ba27-1298-411a-910e-3a32245f1489\", :a, :b, false]}}), 1, 1], :c #ubergraph.core.NodeInfo[#=(clojure.lang.PersistentArrayMap/create {:a #{#ubergraph.core.UndirectedEdge[#uuid \"f18e3829-e53c-4f30-bed8-db5ec9327458\", :c, :a, true]}}), #=(clojure.lang.PersistentArrayMap/create {:a #{#ubergraph.core.UndirectedEdge[#uuid \"f18e3829-e53c-4f30-bed8-db5ec9327458\", :a, :c, false]}}), 1, 1]}) false true #=(clojure.lang.PersistentArrayMap/create {#uuid \"9189ba27-1298-411a-910e-3a32245f1489\" #=(clojure.lang.PersistentArrayMap/create {:weight 2, :price 200, :distance 10}), #uuid \"f18e3829-e53c-4f30-bed8-db5ec9327458\" #=(clojure.lang.PersistentArrayMap/create {:weight 3, :price 300, :distance 20})}) #=(clojure.lang.Atom. nil))"You can recover the ubergraph from such a string with the Clojure function read-string.
One advantage of Option 2 is that it captures the exact UUIDs in the existing graph, as well as any cached hash values. Option 1 merely stores sufficient information about the graph that an equivalent ubergraph can be rebuilt from the information (so, for example, the UUIDs will be different but the nodes/edges/attributes will all contain the same information). Option 1 has the advantage of being somewhat more compact, and amenable as an input to so many serialiazation libraries.
Loom is currently the most important graph library in the Clojure ecosystem. Loom strives to achieve three goals:
Graphs are an important part of my work, and I was disappointed when I discovered that Loom couldn't do many of the things I wanted it to do. For example, I couldn't mix directed and undirected edges, I couldn't have multiple edges between a given pair of nodes, and I couldn't update weights associated with a given edge or have multiple notions of “cost” associated with a given edge.
My first thought was, “Hey, I'll just make an implementation of multi-edge graphs and submit it to Loom.” But as I started looking carefully at Loom's protocols and algorithms, I realized things weren't quite that simple:
In other words, the protocols didn't even support the behavior necessary to implement a multi-edge graph, and even if the protocols were enhanced, very few of the algorithms would actually work on multi-edge graphs – too many assumptions were sprinkled throughout the code base that [src dest] vectors are enough to uniquely identify a given edge.
The ubergraph.alg namespace is a place where the community can help “curate” Loom's algorithms, identifying algorithms from loom.alg that work out of the box on ubergraphs, modifying algorithms from loom.alg that need modification, and writing new algorithms that leverage ubergraph's added capabilities. I have already made good progress on this front, but there are several algorithms that still need to be adapted for Ubergraphs, such as minimum spanning tree and max flow (although Loom's algorithms will likely work on non-multigraph Ubergraphs). I would also welcome any help in creating and adding test cases.
Copyright (C) 2014-2015 Mark Engelberg (mark.engelberg@gmail.com)
Distributed under the Eclipse Public License, the same as Clojure.